[논문리뷰]Feature importance ranking for deep learning(2020)

Feature Importance Ranking for Deep Learning(2020)

Wojtas, Maksymilian, and Ke Chen. “Feature importance ranking for deep learning.” arXiv preprint arXiv:2010.08973 (2020).

Reference count 8

Abstract

• 기능 중요도 순위는 설명 가능한 AI를 위한 강력한 도구가 되었습니다. 그러나 조합 최적화의 특성은 딥 러닝에 큰 도전 과제입니다. 본 논문에서는 고정 크기의 최적 특징 부분 집합을 발견하고 최적 부분 집합에서 이러한 특징의 중요도를 동시에 순위 지정하기 위해 연산자와 선택기로 구성된 새로운 이중망 아키텍처를 제안합니다. 학습하는 동안 연산자는 서로 다른 최적의 하위 집합 후보에 대해 작업하는 연산자의 학습 성능 예측을 학습하는 선택기에 의해 생성된 최적의 기능 하위 집합 후보를 통해 지도 학습 작업에 대해 훈련됩니다. 우리는 두 개의 네트를 공동으로 훈련하고 조합 최적화 문제를 해결하기 위해 학습에 확률론적 로컬 검색 절차를 통합하는 대체 학습 알고리즘을 개발합니다. 배포 시 선택기는 최적의 기능 하위 집합을 생성하고 기능 중요도의 순위를 지정하는 반면 운영자는 테스트 데이터에 대한 최적의 하위 집합을 기반으로 예측을 수행합니다. 합성, 벤치마크 및 실제 데이터 세트에 대한 철저한 평가는 우리의 접근 방식이 여러 최첨단 기능 중요도 순위 및 지도 기능 선택 방법보다 성능이 우수함을 시사합니다. (저희 소스 코드를 사용할 수 있습니다: https:/ / github.com/ maksym33/ FeatureImportanceDL )

Introduction

• 기계 학습에서 기능 중요도 순위(FIR)는 지도 학습 모델의 성능에 대한 개별 입력 기능(변수)의 기여도를 측정하는 작업을 나타냅니다. FIR은 설명 가능/해석 가능한 AI[1]의 강력한 도구 중 하나가 되어 학습 시스템에 의한 의사 결정에 대한 이해와 특정 영역(예: 의학에서 암의 주요 원인이 될 가능성이 있는 유전자)의 핵심 요소 발견을 용이하게 합니다. [2].
• 고차원 실제 데이터의 대상에 대한 상관/종속 및 관련 없는 기능의 존재로 인해 기능 선택 [3]은 잘 알려진 차원 문제의 저주를 해결하고 학습 시스템의 일반화를 개선하기 위해 자주 사용됩니다. 학습 시스템의 성능을 최대화하기 위해 사전 정의된 기준에 따라 최적 기능의 하위 집합이 선택됩니다. 기능 선택은 모집단 또는 인스턴스 수준에서 수행될 수 있습니다. 모집단별 방법은 모집단의 모든 인스턴스에 대해 집합적으로 최적의 기능 하위 집합을 찾는 반면 인스턴스별 방법은 단일 인스턴스에 특정한 두드러진 기능의 하위 집합을 찾는 경향이 있습니다. 실제로 FIR은 최적의 하위 집합에서 해당 기능의 중요도를 순위 지정하여 기능 선택과 항상 밀접하게 연관되어 있으며 기능 선택을 위한 프록시로 사용할 수도 있습니다(예: [2, 4, 5]).
• 딥 러닝은 지능형 시스템 개발에서 매우 강력한 것으로 판명되었지만 “블랙 박스”라고 알려진 특성으로 인해 설명 능력/해석 가능성을 요구하는 작업에 적용하기가 매우 어렵습니다. 최근 딥러닝을 위한 FIR은 대부분의 연구가 인스턴스별 FIR에 초점을 맞추고 [6], 인스턴스별 FIR/특징 선택에 대한 연구는 소수에 불과한 활발한 연구 영역이 되었습니다(예: [7]). 모집단 시나리오에서 기능 선택은 일반적으로 NP-hard인 입력 데이터와 대상 간의 기능적 종속성을 감지하는 데 최적을 찾아야 합니다[8]. 딥 러닝의 높은 수준의 비선형성은 이 조합 최적화 문제를 악화시킵니다.
• 이 논문에서 우리는 심층 학습에서 모집단별 FIR 문제를 다룹니다. 특징 집합에 대해 심층 신경망의 성능을 최대화하는 고정 크기의 최적 특징 부분 집합을 찾고 이 최적 부분 집합에 있는 모든 특징의 중요도를 동시에 순위 지정합니다. . 이 문제를 해결하기 위해 우리는 운영자의 학습 성능 피드백을 통해 최적의 특징 부분 집합을 찾고 특징 중요도 순위를 매기는 선택기 네트워크에서 제공하는 최적의 부분 집합 후보를 통해 지도 학습 작업에 대해 운영자 네트워크가 작동하는 새로운 이중 네트워크 신경 아키텍처를 제안합니다. 두 개의 네트가 교대로 공동으로 훈련됩니다. 학습 후 선택기 네트는 최적의 기능 하위 집합을 찾고 기능 중요도의 순위를 지정하는 데 사용되는 반면 연산자 넷은 테스트 데이터에 대한 최적의 기능 하위 집합을 기반으로 예측을 수행합니다. 비교 연구를 통한 합성, 벤치마크 및 실제 데이터 세트에 대한 철저한 평가는 딥 러닝을 활용한 우리의 접근 방식이 여러 최첨단 FIR 및 지도 기능 선택 방법보다 성능이 우수함을 보여줍니다.

Related Research

• 딥 러닝의 맥락에서 FIR에는 세 가지 방법이 있습니다. 정규화, 탐욕 검색, 평균 입력 기울기.
• DFS(Deep Feature Selection)[7]는 정규화된 선형 모델[9, 10] 뒤에 동일한 아이디어로 FIR에 대해 제안되었습니다. DFS는 다음과 같은 몇 가지 문제를 겪고 있습니다. 최적의 정규화 하이퍼파라미터와 소실 그라디언트를 찾는 데 높은 계산 부담. 더욱이, 가중치 축소 아이디어[9, 10]는 축소된 가중치를 기능 중요도로 사용하는 것이 이론적으로 선형 모델에서만 정당화될 수 있기 때문에 입력 기능과 대상 간의 복잡한 종속성에 대해 항상 작동하지 않을 수 있습니다.
• FIR을 위한 딥 러닝에 탐욕 검색 방법(예: 순방향 부분 집합 선택(FS)[11])을 적용하는 것은 간단해 보입니다. 분명히, 이 방법은 필연적으로 매우 높은 계산 비용을 발생시키고 차선의 결과로 끝날 수 있습니다.
• 마지막으로, 일부 인스턴스별 FIR 방법은 FIR 및 전역 집계를 위해 개별 인스턴스에서 추출된 모든 돌출 맵의 평균을 사용하는 평균 입력 기울기(AvGrad)[12]와 같이 모집단별 방법으로 변환되었습니다[13, 14, 15]. 다른 집계 메커니즘을 사용하여 모집단별 기능 중요도 순위를 달성합니다. 지역 설명은 인스턴스 수준에서 구체적이고 종종 인스턴스 수준에서 글로벌 설명과 일치하지 않기 때문에 인스턴스별 FIR 결과의 단순 누적은 인스턴스별 FIR에서 작동하지 않을 수 있습니다. 대조적으로, 우리의 방법은 위에서 언급한 모든 한계를 극복할 것입니다.

Method

1. Formulation

• D = {X,Y}가 지도 학습에 사용되는 데이터 세트라고 가정합니다. 이 데이터 세트에서 (x , y )는 training example입니다. 여기서 x ∈X는 d 특성의 벡터이고 y ∈Y는 해당 target입니다.

• m ∈M이 0/1 요소의 d차원 이진 마스크 벡터를 나타낸다고 가정합니다.

  (

  m

  _0 = s, s < d 및

  M

  = ( ds ) ).

  따라서 이러한 마스크 벡터를 사용하여 특성 부분 집합을 나타낼 수 있습니다.

  { x ⊗m}x∈X

  여기서 ⊗는 x ∈ X 인스턴스에 대해 s 특성의 부분 집합을 생성하는 Hadamard 곱을 나타냅니다.

• Q(x, m )는 기능 하위 집합 {x ⊗m}을 통해 D에 대해 훈련된 학습 시스템의 인스턴스 level의 성능을 수량화합니다. 그러면 기능 중요도 순위(FIR)는 다음과 같이 공식화될 수 있습니다 :

  

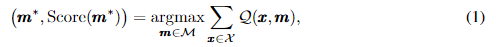
• 여기서 m* 은 optimal feature subset의 지표입니다. FIR 알고리즘에 의해 발견되고 Score(m*)는 이 optimal subset에서 선택된 모든 특징의 중요성을 수량화합니다.

• 이상적으로 FIR 접근 방식은 다음을 수행할 수 있어야 합니다.

  1) input feature와 target 간의 기능적 종속성을 감지합니다.

  2) 학습 성과에 대한 기여도를 반영하기 위해 선택된 모든 feature의 중요성을 평가합니다. \

  3) 테스트 데이터에서 감지된 functional independencies와 기능 중요도 순위를 유지(preserve)합니다.

2. Model Description

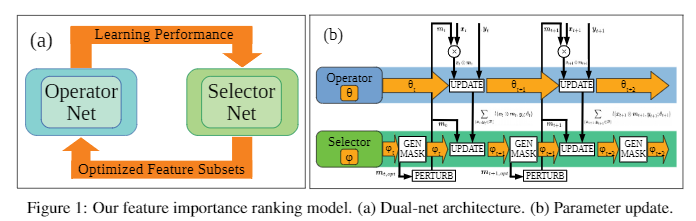
• Eq.(1)에 명시된 FIR 문제를 Sect. 3.1에서 우리는 그림 1(a)와 같이 이중망, 연산자 및 선택기의 딥러닝 모델을 제안합니다.
• 오퍼레이터 네트는 선택자 네트가 제공하는 주어진 기능 하위 집합에 대한 지도 학습 작업을 수행하는 데 사용됩니다.
• 선택기 네트워크는 학습 중 최적의 기능 하위 집합 후보에 대해 작업하는 연산자 네트워크의 성능 피드백을 기반으로 최적의 기능 하위 집합을 찾는 학습을 위해 지정되었습니다.
• 오퍼레이터와 셀렉터 네트는 FIR의 시너지 효과에 도달하기 위해 대안적인 방식(섹션 3.3)으로 공동으로 훈련됩니다.
• 기술적으로 오퍼레이터는 예를 들어 다층 퍼셉트론(MLP) 또는 컨볼루션 신경망(CNN)과 같은 주어진 작업에 대해 θ, fO(θ;x, m)로 매개변수화된 심층 신경망으로 수행됩니다. 이 네트워크는 f O : X × M → Y를 학습하기 위해 다양한 기능 하위 집합을 기반으로 D에 대해 학습됩니다. 학습(섹션 3.3 참조) 후, 훈련된 오퍼레이터 네트 fO(θ* ;x, m)가 예측을 위한 테스트 데이터에 적용됩니다. 여기서 θ는 오퍼레이터 네트의 최적 매개변수입니다. m*은 훈련된 셀렉터 네트에 의해 생성됩니다(섹션 3.4 참조).

• 셀렉터는 ϕ, f S(ϕ;m)로 매개변수화된 MLP로 구현됩니다.

  Eq.(1)에 정의된 바와 같이, 선택된 최적의 feature subset은 모든 x ∈X에 대해 Q(x, m)로 정량화된 오퍼레이터의 평균 성능을 최대화해야 합니다.

  따라서 우리는 셀렉터 네트가 각기 다른 feature subset에 대한 오퍼레이터 네트의 평균 성능 예측을 학습하기를 원합니다. ie, fS : M→ R.

  적절하게 훈련된 후(3.3절 참조), 최적 매개변수 ϕ∗ , fS (ϕ∗ ;m)의 훈련된 선택기 네트워크에서 작동하는 알고리즘을 사용할 수 있습니다. optimal feature subset을 생성하기 위해서.

  optimal feature subset은 다음이 지표가 된다. m *

  그리고 Score(m *)를 달성하기 위한 기능 중요도 순위를 지정한다. (섹션 3.4 참조0).

3.3 Learning Algorithm

• 본질적으로 Eq.(1)에 정의된 FIR은 조합 최적화 문제입니다. 최적화를 위한 공짜 점심 없음 이론[19]에 따르면 조합 최적화 설정에서 예상되는 임의 전략보다 더 나은 알고리즘은 없습니다. 따라서 우리의 학습 알고리즘은 철저한 검색을 피하기 위해 소수의 후보 특징 부분 집합 M’ ⊂M에 노이즈를 주입하여 향상된 확률론적 지역 검색 절차로 학습을 활용하여 개발되었습니다.

• 훈련 데이터 세트의 경우 D = {X,Y} = { ( x , y ) } 마스크 부분 집합 M ′ 는 각 훈련 데이터셋 (x, y) ∈ D를

  M ′

  로 변경합니다. (예: { (x ⊗ m, y) } m∈M ′) . 따라서 operator 및 selector net에 대한 M’(학습 중 변경)에 대한 손실 함수는 각각 다음과 같이 정의됩니다.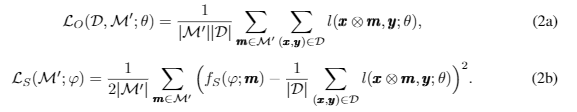

  

• 여기서 l(x⊗m, y;θ)은 이진/다중 클래스 분류를 위한 instance-wise 크로스 엔트로피/카테고리컬 크로스 엔트로피 손실 또는 회귀에 대한 평균 제곱 오차(MSE) 손실입니다.
• Eq.(2b)에서 우리는 학습 성능 Q(x, m)을 특성화하기 위해 오퍼레이터 네트 손실 l(x ⊗ m, y;θ)를 활용합니다. l(x⊗m, y;θ)을 최소화합니다.
• Sect.3.2에서 설명했듯이, 학습하는 동안 operator net은 다양한 최적의 feature 하위 집합 후보를 나타내는 최적의 표시 부분 집합 M’을 제공하기 위해 selector net에 의존하는 반면, selector net은 operator net, l(x⊗m, y;θ)에서 모든 m에 대하여 성능 피드백을 필요로 합니다.

• 따라서 학습 모델의 두 네트는 교대로 학습해야 합니다. 아래에서 우리는 두 단계의 학습 알고리즘의 주요 학습 단계를 제시하고 수도 코드는 보충 자료의 Sect.D에서 찾을 수 있습니다.

  

Phase I : Initial Operator Learning via Exploration

• 처음부터 다른 기능 하위 집합에 대해 다른 성능을 안정적으로 산출할 수 있을 때까지 여러 에포크에 대해 소수의 무작위 기능 하위 집합을 사용하여 연산자 네트워크를 훈련하기 시작합니다.

• 각 에포크에서 M에서 서로 다른 마스크 M’1의 하위 집합을 무작위로 그립니다.

  

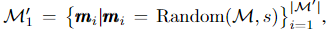
  Random(M,s)은 M에서 s개의 요소와 d−s개의 0요소로 구성된 d차원 마스크를 무작위로 그리는 함수입니다.

• θ가 SGD(stochastic gradient Decent)에 의해 훈련되면, θ’‘에 의해 업데이트됩니다. 여기서 η는 학습률입니다.

  

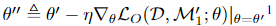
• E1 에포크 후에 다음과 같이 셋팅합니다.

  

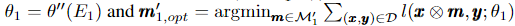
  이는 Phase II-A단계의 시작에 사용됩니다.

Phase II-A: Selector Learning via Operator’s Feedback.

• 그림 1(b)와 같이 오퍼레이터는 t단계에서 셀렉터에 대한 training example을 제공합니다.

  

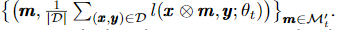
• 셀렉터 네트의 파라미터 ϕ는 다음 식에 의해 업데이트 됩니다.

  

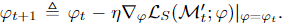
• 그런 다음, t+1 단계에서 오퍼레이터 학습을 위해 새로운 마스크 부분 집합 M’t+1 을 생성하기 위해 exploration-exploitation 전략을 채택합니다. 따라서 M′t+1은 두 개의 상호 배타적인 부분 집합으로 나뉩니다.

  

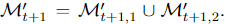
• Exploration : M’ t+1,1은 과적합을 피하기 위해 탐색을 통해 생성됩니다.

  

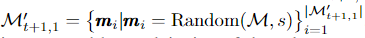
• Exploitation : M′t+1,2은 셀렉터의 exploitation에 의해 생성됩니다. 다음과 같은 방법을 통해서.

  • a) Generation of an optimal subset

    d차원의 m0 = (0.5, 0.5, …, 0.5)이면 모든 feature가 선택될 기회가 동일하므로 미분시 다음과 같다.

    

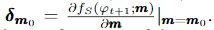
    더 큰 그래디언트의 input feature가 오퍼레이터의 학습 성능에 더 많이 기여함에 따라 다음 식에 의해 그래디언트를 기반으로 top s 기능을 찾을 수 있습니다.

    

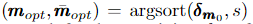
    여기서 m_opt는 top s 기능을 나타내는 마스크이고 ¯ m_opt는 나머지 d-s 기능에 대한 마스크입니다.

    검증 절차를 거친 후 t+1 단계에 대한 mt+1,opt를 얻습니다.

  • b) Generation of optimal subset candidates via perturbation.

    최적의 부분집합 m t+1,opt가 local optimum 일 수 있으므로 섭동 함수 Perturb(m_opt,s_p)에 의해 더 최적의 부분집합 후보를 생성하기 위해 노이즈를 추가로 주입합니다.

    

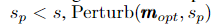
  • c) Formation of optimal subset candidates.

    a)와 b)를 조립하면 다음과 같습니다.

    

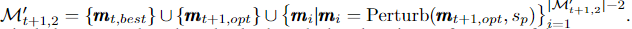
  • 여기서 우리는 항상 마지막 단계(단계 t)에서 오퍼레이터 네트의 최상의 학습 성능으로 이어지는 부분집합인 mt_best를 현재 단계(단계 t+1)에서 가장 중요한 부분집합 후보로 포함하여 오퍼레이터 학습 진행 꾸준히 만들도록 한다. mt_best는 mt_opt가 아닐 수 있습니다.

Phase II-B: Operator Learning via Optimal Subset Candidates from Selector.

• 단계 t에서 II-A 단계의 훈련을 완료한 후, 셀렉터 네트는 그림 1(b)와 같이 오퍼레이터 네트에 대한 최적의 부분집합 후보를 제공합니다.

  

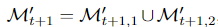
• 따라서 t+1 단계에서 오퍼레이터 네트는 SGD를 사용하여 M’ t+1을 기반으로 훈련됩니다.

  

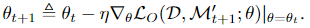
• 그림 1에서 볼 수 있듯이 우리의 대체 알고리즘은 미리 지정된 정지 조건이 충족될 때까지 오퍼레이터와 셀렉터 네트가 2단계에서 공동으로 훈련되도록 합니다.

Deployment

• 학습이 완료되면 오퍼레이터와 선택기 네트워크의 최적 매개변수 θ ∗ 및 ϕ ∗ 를 얻습니다.
• 훈련된 셀렉터 네트를 사용하여 다음과 같이 단계 II-A에서 사용된 것과 동일한 절차로 최적의 특징 부분 집합을 찾습니다.
• 1) 기울기를 계산합니다

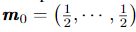
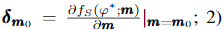
• 2) 다음 식에 의해 top s개의 feature를 찾습니다. 여기서 m* 은 상위 s개의 feature의 optimal subset을 의미합니다.

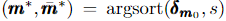
• 3) m * 의 최적성을 보장하기 위해 단계 II.A에 설명된 검증 절차를 거칩니다.

Conclusion

• Selector에서 Feature Selection + Operator에서 예측을 수행하는 듀얼넷 구조의 Feature Importance Ranking
• 논문 구현