[논문리뷰] Rainbow: Combining Improvements in Deep Reinforcement Learning(2018)

1. 논문 선정 이유 및 개요

• 이 연구는 AAAI에 등재됐으며, 인용횟수가 501회에 달한다.
• 이 논문을 선택한 이유는 DQN을 강화한 6가지의 기법을 적용한 Rainbow DQN을 내세웠기 때문이다. DDQN, Dueling DQN, PER, Multi-step Learning, Distributional RL, Noisy Net 6개의 기법을 다시 톺아볼 수 있기 때문에 이 논문에 대한 review paper를 작성하면서 강화학습의 flow를 정리하고자 한다. Rainbow DQN에서 쓰인 6가지의 DQN을 살펴보고(앞에서 본 DQN은 생략) Rainbow DQN의 성능을 보고자 한다.
• 이 연구는 DQN 알고리즘에 대한 6가지 확장과 그들의 조합을 실험하여 Rainbow DQN을 구현하였다. 57개의 Atari game에서 DQN의 성능 비교를 해본 결과, Rainbow DQN의 performance가 가장 좋았다.

2.Double Q-learning (DDQN)

2.1 Challenge

• Q-learning은 maximization 방법으로 Q를 업데이트하기때문에, Q값을 과대 평가하게 되어 Q값이 낙관적인 예측을 하게 되는 문제가 있다. 이로 인해 학습 효율이 떨어진다.
• 그 이유를 보면, max 연산자는 행동을 선택하고 평가하는 데 동일한 값을 사용하기 때문이다. 이에 따라 상태 s에서 모든 동작에 대한 Q값을 추정할 때, 추정된 Q값은 약간의 오차(noise)가 생기게 된다. 이 오차로 인해 최적 행동이 아닌 차선의 행동이 선택될 수 있다

2.2 구현

• Target과 Evaluation을 분리한다. 즉, Double Q-learning은 online Q-network를 최대화하는 행동 값을 target Q-network의 입력으로 하여 target Q값을 계산함으로써 target Q값의 과대평가를 방지한다.
• 이러한 concept에 따라, 다음과 같이 Loss Function을 조정한다.
  
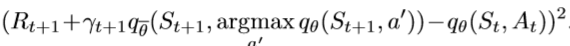
• 위와 같이, 하나의 큐함수를 사용하여 행동을 선택하고, 다른 큐함수로 행동을 평가한다. 여기에서main Q함수는 Q값이 max가 되는 action을 고르고, target Q는 보상을 추정하고 업데이트 한다.
• 2개의 Q함수를 사용함으로써, max함수에 의한 positive bias를 줄여주게 된다.

3. Prioritized Replay (PER)

3.1 Challenge

• DQN은 경험 리플레이로 훈련 샘플 간의 상관관계를 제거한다. 그러나 경험 리플레이 메모리에서 transitions를 균일하게 Sampling하는 것은 비효율적이다. Sampling시, 학습이 더 필요한 transitions을 선택하는 것이 더 이상적인 방법이다. 중요도에 따라 전이와 샘플의 우선순위를 지정하면, 네트워크가 효과적으로 학습할 수 있다.

3.2 구현

• PER에서는 전이의 우선순위를 결정할 때, 높은 TD-에러가 있는 전이를 중요하게 고려한다. TD-에러는 추정된 Q값과 실제 Q값 간의 차이를 의미한다. 높은 TD-에러가 있는 전이는 예상 밖의 전이이므로 학습이 필요하다. 즉 실패하는 문제에 우선순위를 부여해, 잘못된 부분을 우선 집중해 문제를 해결한다는 취지이다.
• PER은 마지막으로 발생한 TD-Error와 관련된 확률로 transition을 sampling하고, 경험 리플레이로부터 경험을 균일하게 추출하여 학습한다.

3.3 method

• 논문에서는 PER 적용 시의 문제점을 보완하고 있다. PER 적용 시, 우선순위를 임의로 지정해서 sampling 했기 때문에 실제 환경에서의 transition의 분포와 sampling 된 transition의 분포 사이에 차이가 발생한다. 이는 학습 시 bias가 발생하는 원인이 된다.
• 따라서 본 연구에서는 신경망 update 시 Importance-sampling weight(β)로 보정을 해준다.

4. Dueling Network (Dueling DQN)

4.1 Challenge

• DQN의 Q함수는 에이전트가 “상태”에서의 좋은 정도를 나타낸다. 즉, Q함수 Q(S,A)는 어떤 State에서의 가치만을 나타낸다.
• 그러나 대부분의 상태에서 가능한 모든 행동에 대한 가치를 추정하는 것은 중요하지 않다. 특히 행동 공간이 큰 경우에 모든 행동에 대한 가치가 중요하지는 않다.
• Dueling networks는 Q 값을 특정상태에서의 가치(Value)와 그 상태에서 취할 수 있는 다양한 행동에 대한 이득(Advantage)을 분리하고자 한다. (Architecture Modification)

4.2 구현

• 어드밴티지 함수는 에이전트가 다른 행동과 비교해 행동 a를 수행하는 것이 얼마나 좋은지를 나타낸다. 따라서 “상태”가 아닌 “행동”의 좋은 정도를 확인한다.
• Dueling network는 두 computation으로 줄기를 나눈다 :
• 가치함수 스트림 : 상태에 많은 수의 행동이 있고 각 행동의 값을 추정하는 것이 크게 중요하지 않을때 유용하다.
• 어드밴티지함수 스트림 : 선호되는 행동을 결정해야할 때 유용하다

5. Multi-step Learning

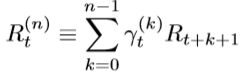
• DQN은 target Q 값을 계산할 때 바로 다음 상태, 즉 1-step 부트스트랩 후의 보상을 사용한다.
• 이를 확장하여 n-step 부트스트랩 후의 보상 정보를 이용하여 학습하게 되면, 즉 multi-step learning, 학습 안정성과 속도가 개선된다

6. Distributional RL(C51)

6.1 Challenge

• DQN은 Q 값의 기대치를 이용한다. 이 경우, MDP에 내재된 랜덤성을 활용하기 어렵다.
• Return의 기대치 대신, Return의 분포를 근사하는 방법을 학습하고자 한다.

  6.2 구현

• General Q(s,a) = R(s,a) + 𝛾Q(s’, a’) Distributional Z(s,a) = R(s,a) + 𝛾Z(s’, a’)
• 이 때 Loss Function은 Target value distribution과 현재 value distribution간의 차이를 줄이는 방향으로 학습하게 된다.
• KL-Divergence(쿨백-라이블러 발산은 두 확률분포의 차이를 계산하는 데에 사용하는 함수)을 통해 학습을 진행한다.
  
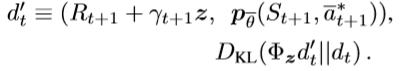
• Distributional RL은 하나의 평균값 대신 보상의 분포를 이용하는 방법으로 학습 성능의 개선뿐만 아니라 에이전트가 위험이 큰 행동을 피할 수 있게 하기 때문에 안전한 에이전트 설계가 가능해진다

7. Noisy Network

7.1 Challenge

• DQN은 ε-탐욕 정책을 이용한다. 하지만 ε-탐욕 정책은 현재 에이전트가 처한 상황에 관계없이 랜덤 행동을 출력하기에 종종 비효율적인 탐험을 할 뿐만 아니라 ε 값 설정에 대한 문제도 존재한다.
• 몬테주마의 복수와 같은 게임을 예로 들면, 첫 보상(열쇠)을 얻기 위해 많은 조치를 취해야한다.

7.2 구현

• Noisy Nets는 정책 신경망 학습 시 정책 신경망의 가중치와 편향에 잡음을 부여하는 신경망(Noisy Nets)을 함께 학습함으로써 에이전트 행동 랜덤성이 에이전트가 처한 상태에 따라 그리고 학습 진행 시간에 따라 자동으로 적응되는 이점(예, 학습이 진행됨에 따라 랜덤성이 감소하며 greedy 선택을 촉진함)을 얻게 된다
  

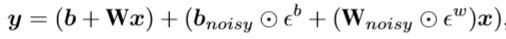
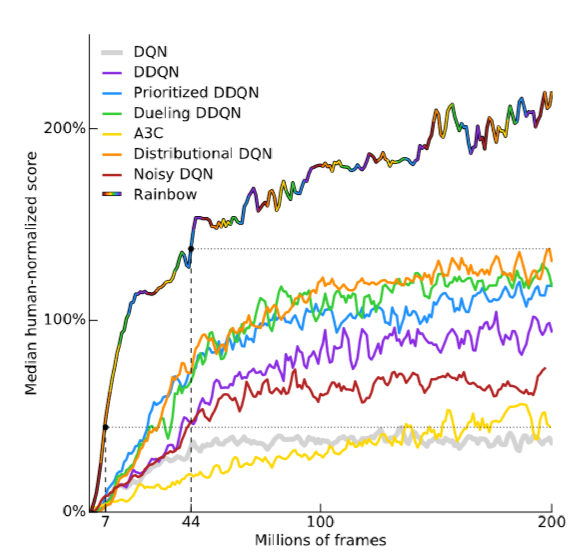
8. The Integrated Agent (Rainbow DQN)

• Rainbow DQN은 위의 언급된 6 extenstion DQN이 모두 적용된 버전이다.
• 57개의 Atari게임에서 기존 DQN에 비해 월등한 성능을 보였으며, muti‑step 또는 priority를 제외하였을때 레인보우의 성능이 떨어졌다.
  

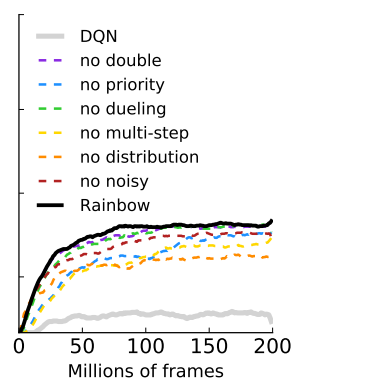
9. 분석 및 개인 견해

• Rainbow DQN은 위 DQN과 더불어 6가지 확장을 조합하여 성능을 극대화하였다. 6가지의 확장은 Double Q-learning, Prioritized Experience Replay(PER), Dueling DQN, Multi-step Learning, Distributional RL(C51), Noisy Network이다.
• Double Q-Learning은 Q함수의 과대평가를 막기 위해, Q함수를 두 개로 분리한다. main Q함수는 Q값이 최대가 되는 행동을 선택하고, target Q함수는 보상을 추정해 업데이트한다. 이로써 max연산에 대한 bias를 줄여주게 된다.
• Prioritized Experience Replay(PER)는 첫번째 리뷰논문에서의 DQN의 경험 리플레이에서 샘플링 시 우선순위를 주어 학습의 효율성을 극대화한다. PER은 DQN의 sampling시, 더 학습이 필요한 샘플의 우선순위를 지정한다.
• Dueling DQN은 에이전트가 취할 수 있는 행동에 대한 보상을 계산해준다. 즉, 첫번째 리뷰논문에서의 DQN이 Q함수를 통해 “상태”의 좋은 정도만 확인하는 반면, Dueling DQN은 “행동”의 좋은 정도를 확인하는 어드밴티지 함수를 추가한다. 이로써, 선호되는 행동을 결정할 수 있다.
• Multi-step Learning은 Rainbow DQN에서 n-step 부트스트랩 이후의 보상 정보를 이용하여 학습할 수 있게 한다.
• Distributional RL(C51)은 첫번째 리뷰논문에서의 DQN이 Q값의 기대치를 스칼라로 근사하는 것과 달리, 기대치의 확률 분포를 근사한다. 즉, 하나의 평균값 대신 보상의 분포를 이용함으로써, 첫번째 리뷰논문의 DQN에서보다 학습 성능이 개선될 수 있으며 에이전트가 위험을 회피할 수 있게 한다.
• Noisy Network는 첫번째 리뷰논문에서의 DQN이 ε-탐욕 정책을 이용해 종종 비효율적인 탐색을 하는 것에 대한 대안이 된다. Noisy Network는 에이전트의 행동이 처한 상태나 학습 진행시간에 따라 자동으로 적응되는 이점이 있다.
• 위의 6가지 확장된 DQN을 조합한 Rainbow DQN은 첫번째 논문에서의 DQN은 물론 각기 6가지의 확장된 DQN보다 성능이 상회함을 알 수 있었다.

Reference

• Hessel, Matteo, et al. “Rainbow: Combining improvements in deep reinforcement learning.” Thirty-Second AAAI Conference on Artificial Intelligence. 2018. https://www.aaai.org/ocs/index.php/AAAI/AAAI18/paper/viewPaper/17204
• Van Hasselt, Hado, Arthur Guez, and David Silver. “Deep reinforcement learning with double q-learning.” Thirtieth AAAI conference on artificial intelligence. 2016. https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/viewPaper/12389
• Wang, Z., Schaul, T., Hessel, M., Van Hasselt, H., Lanctot, M., & De Freitas, N. (2015). Dueling network architectures for deep reinforcement learning. arXiv preprint arXiv:1511.06581. https://arxiv.org/abs/1511.06581
• Bellemare, Marc G., Will Dabney, and Rémi Munos. “A distributional perspective on reinforcement learning.” Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017. https://arxiv.org/abs/1707.06887