[논문리뷰]BEM-A3C : Practical Implementation and Evaluation of Deep Reinforcement Learning Control for a Radiant Heating System(2018)
Why this paper?
- 이전 논문에서 건물 에너지 예측에 적용한 A3C 알고리즘 부분을 중점적으로 설명함 → A3C 알고리즘 설명을 덧붙여서 건물 에너지 예측에 어떻게 적용했는지 살펴봄
Formal Paper Proposed Process
- HVAC Modeling : EnergyPlus라는 시뮬레이션 툴로, 시뮬레이션 환경을 만든다
- Model Calibration : 만들어놓은 시뮬레이터가 실제 데이터와 비슷하도록 보정한다
- DRL Training : 보정된 시뮬레이터로 최적의 제어 정책을 훈련시킨다. A3C 기반으로. ← 오늘 집중 리뷰할 부분
- Deployment : 훈련된 RL 에이전트를 static 하게 배포함
- Performance : 작년 겨울과 올해 겨울은 더 춥거나 더 더울 수 있으므로 Normalization 이후 둘의 난방 수요를 비교한다.
A3C
A3C 개요
- A3C 배경) DQN이 부족한점 : 메모리 과다 사용, 학습속도 느림, 가치함수에 대한 greedy policy이므로 불안정한 학습과정
- A3C : Asynchronous Advantage Actor-Critic
- 샘플사이의 상관관계를 비동기 업데이트로 해결 ( DQN은 Replay Buffer를 사용했음)
- 리플레이 메모리를 사용하지 않음
- policy gradient 알고리즘 사용 가능(Actor-Critic)
- 상대적으로 빠른 학습 속도(여러 에이전트가 환경과 상호작용함)
- A3C = 비동기 + Actor-Critic
- Actor-Critic = REINFORCE + 실시간 학습
- REINFORCE = 몬테카를로 Policy gradient
- 따라서 policy graident → REINFORCE → Actor-Critic → A3C → 난방시스템에 적용 이 단계로 알아보려함
A3C에 대한 직관적 이해
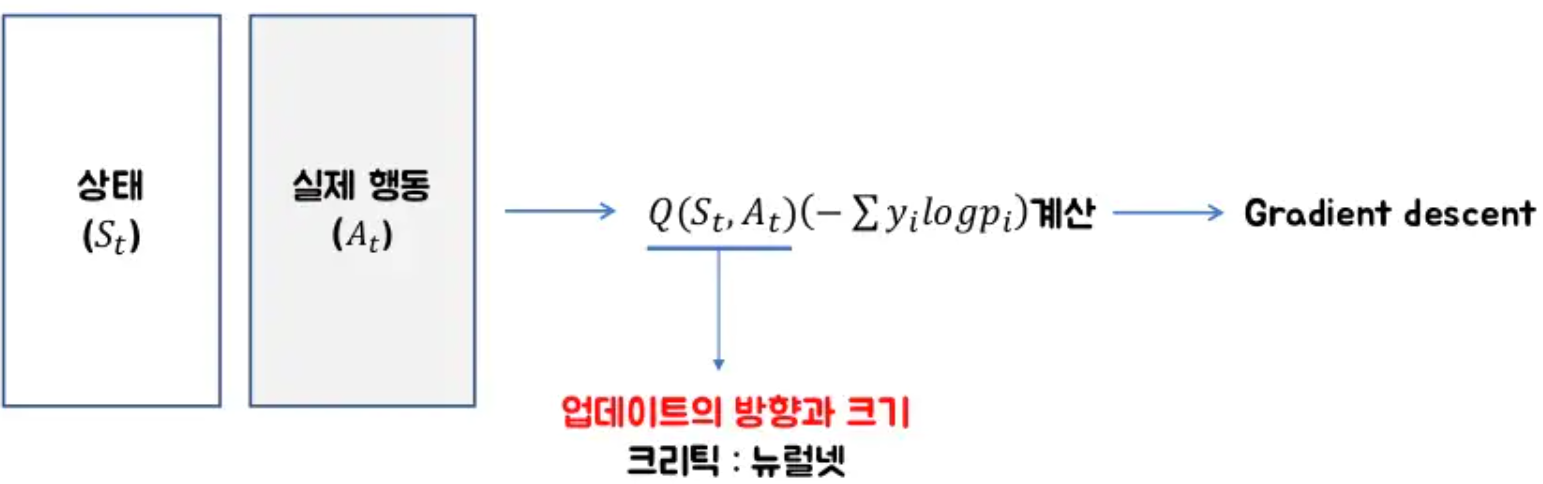
- 지도학습의 크로스 엔트로피 : input과 label에 대해 예측p와 정답y가 얼마나 다른지 계산해서 gradient descent함
- 강화학습의 크로스 엔트로피 : input 상태벡터와 실제행동 a에 대해 각 행동을 할 확률 예측 p와 실제 에이전트가 한 행동 정답 y가 얼마나 다른지 계산해서 → 나의 예측을 실제 행동에 가깝게 gradient descent하여 만든다. → 업데이트의 방향성이 중요함
-
Actor-Critic : 정답이 되는 각 행동이 실제로 좋은지, 좋다면 얼마나 좋은지 알 수 있을까? → 상태벡터와 실제행동 a에 대해 Q함수로 업데이트의 방향과 크기를 계산한다.
-
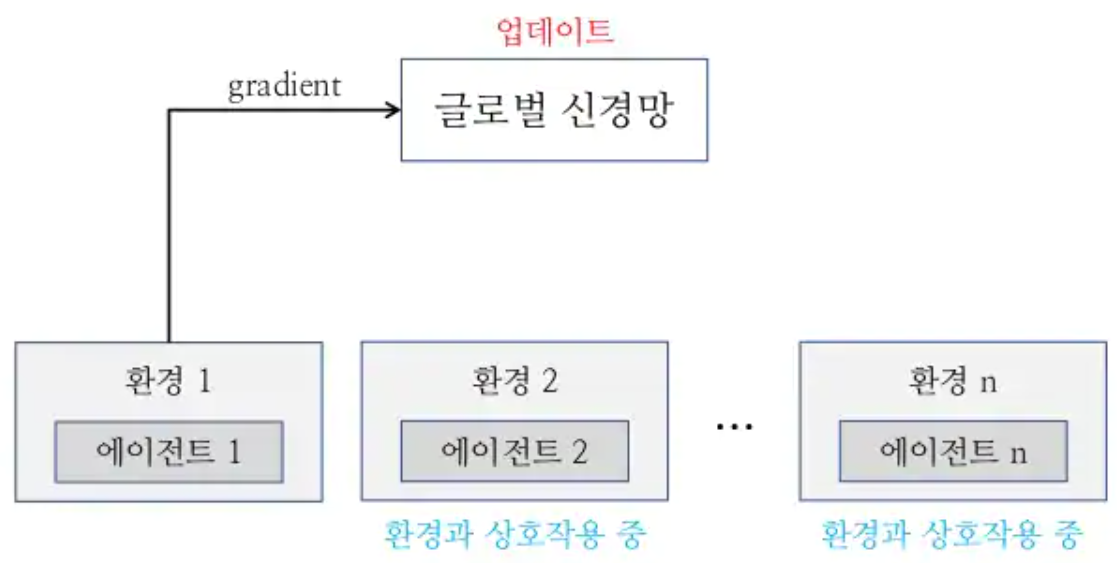
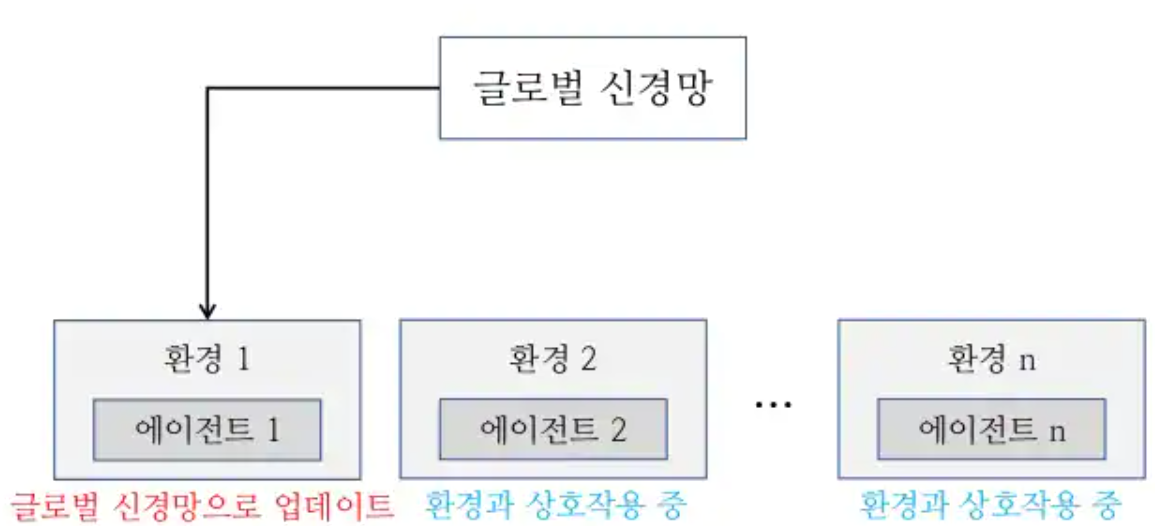
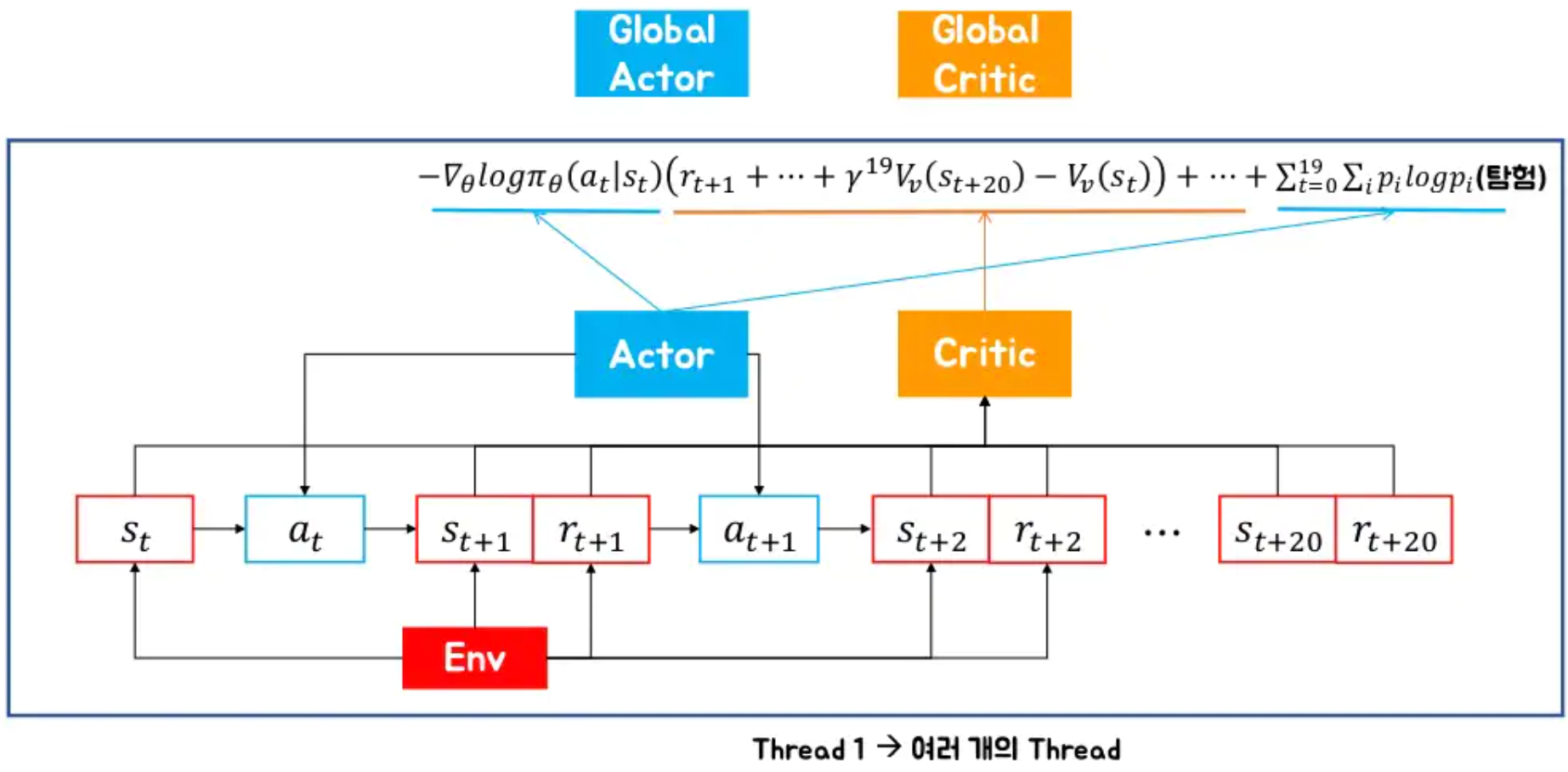
AC3 : 여러개의 에이전트를 만들어서 각각 환경에서 gradient를 계산하고, 비동기적으로 global network를 업데이트.

-
비동기적으로 global network를 업데이트
Policy Gradient(PG)
- 정책을 업데이트 하는 기준 : 목표함수 → 정책의 근사화 (큐 함수가 아니라)
- 목표함수에 따라 정책을 업데이트하는 방법 : Gradient ascent
- 정책의 근사화
- 각 상태에 대한 정책을 가지는 것은 힘듬. 따라서 행동 = f(상태) → f가 정책이됨
-
인공신경망으로 큐함수가 아닌 정책을 근사함.
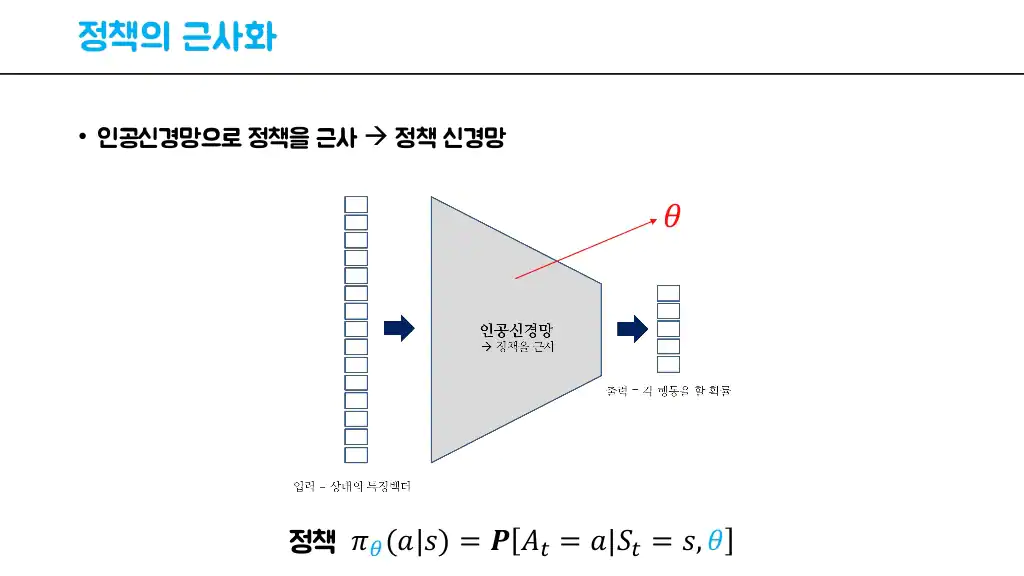
- 목표 함수
- 가치 기반 강화학습에서는 가치 함수 : 매 스텝마다 에이전트가 행동을 선택하는 기준
- 정책 기반 강화학습에서는 목표 함수 : 정책을 업데이트할 때마다 어떤 방향으로 업데이트할 지에 대한 기준 J(θ)

REINFORCE
- 한 에피소드를 현재 정책에 따라 실행
- Trajectory(경로)를 기록
- 에피소드가 끝난 후 Gt(할인이 적용된 누적보상) 계산
- Policy gradient를 계산해서 정책 업데이트
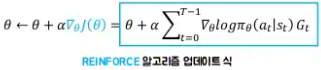
- (1~4) 반복
- 에피소드마다 업데이트하므로 → 몬테카를로 Policy graident = REINFORCE
- 문제가 있다
- Variance가 높다 : 에피소드가 길어질수록 특정 (s,a)에 대한 return의 변화가 커짐.
- 에피소드마다 업데이트가 가능하다. online이 아니다. - 그래서
- 몬테카를로 → TD(Temporal-Difference)
- REINFORCE → Actor-Critic
Actor-Critic
- REINFORCE 식에서 Expectation을 쪼개보자
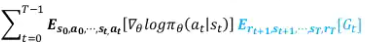
파란색 부분은 Q함수임
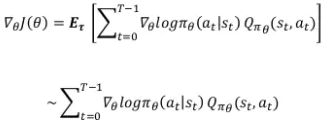
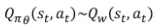
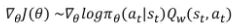
- Advantage 함수 = “큐함수 - 베이스라인” → variance를 낮춰준다.
- 큐함수 : 특정 상태, 특정 행동에 따른 값
- 가치함수 : 특정 상태, 전반적 행동에 따른 값 → 베이스라인
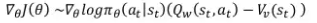
-
Q와 V를 둘 다 근사하는 건 비효율적
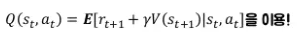
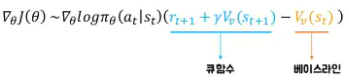
-
정리하면

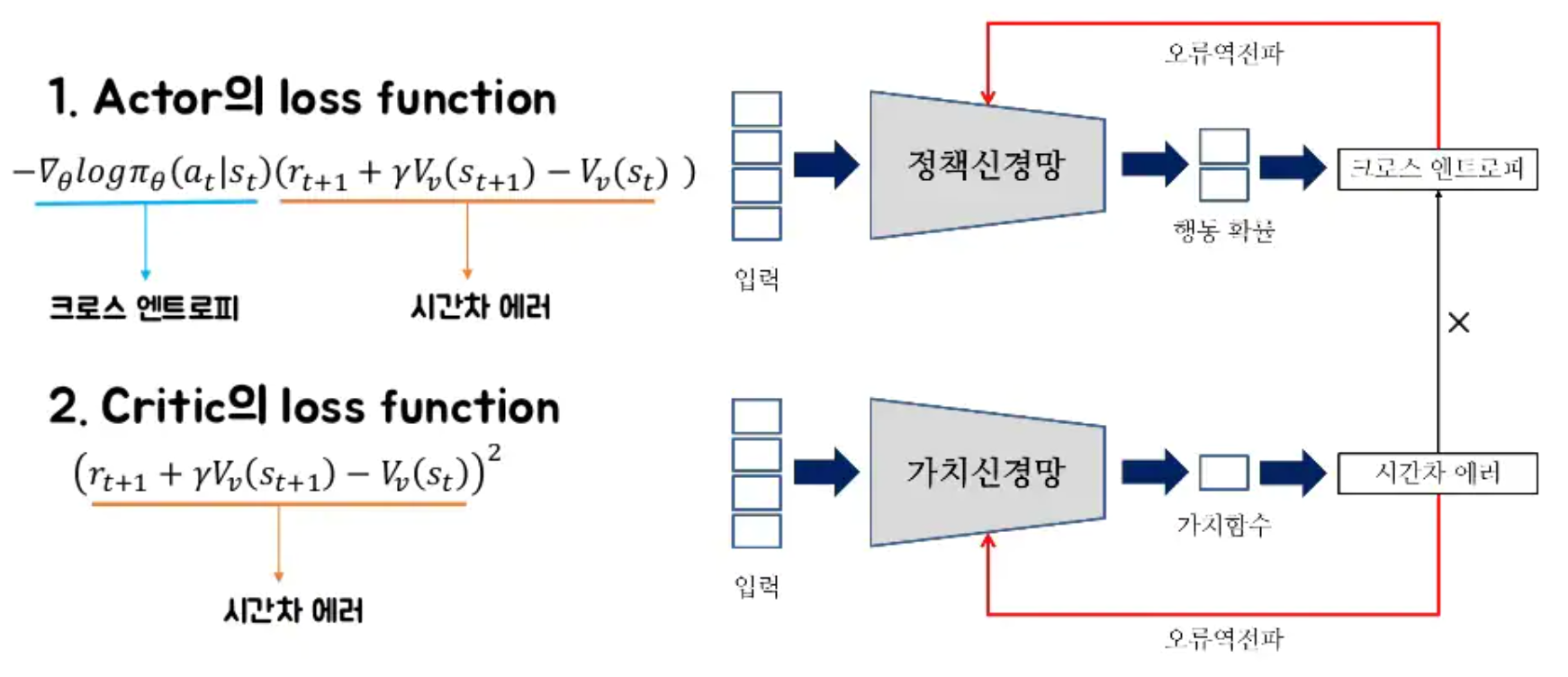
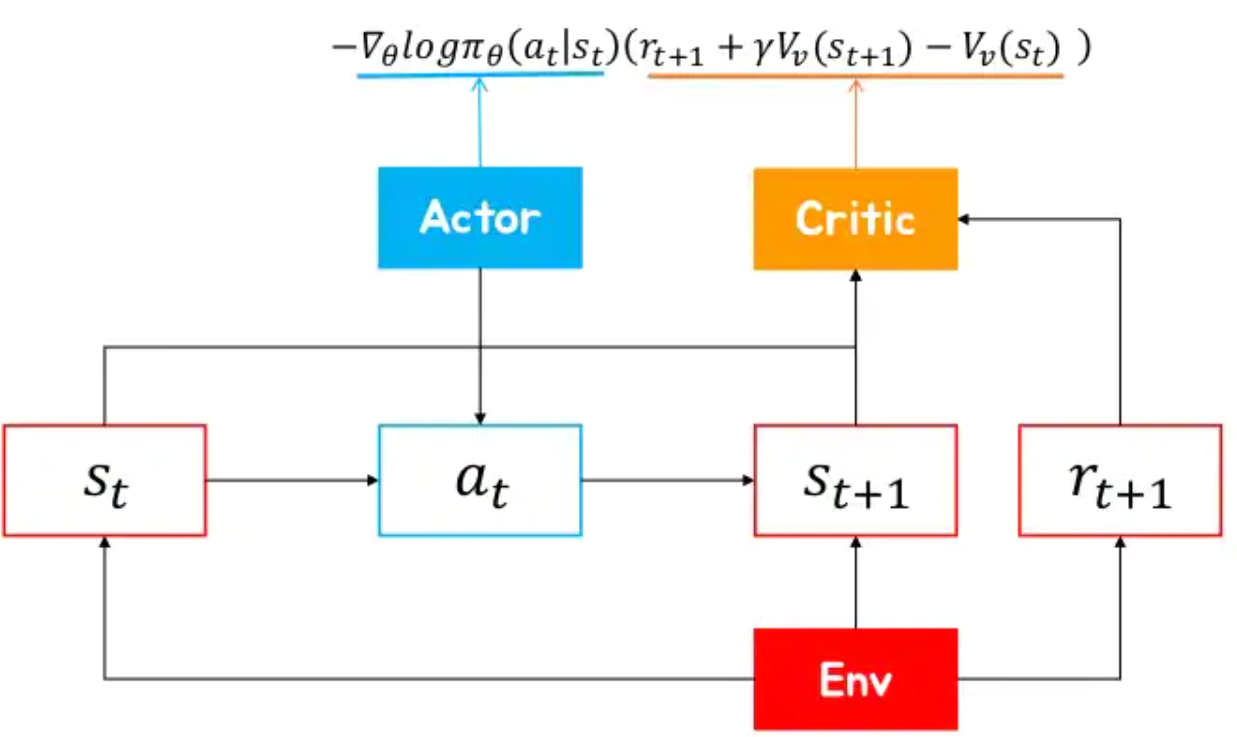
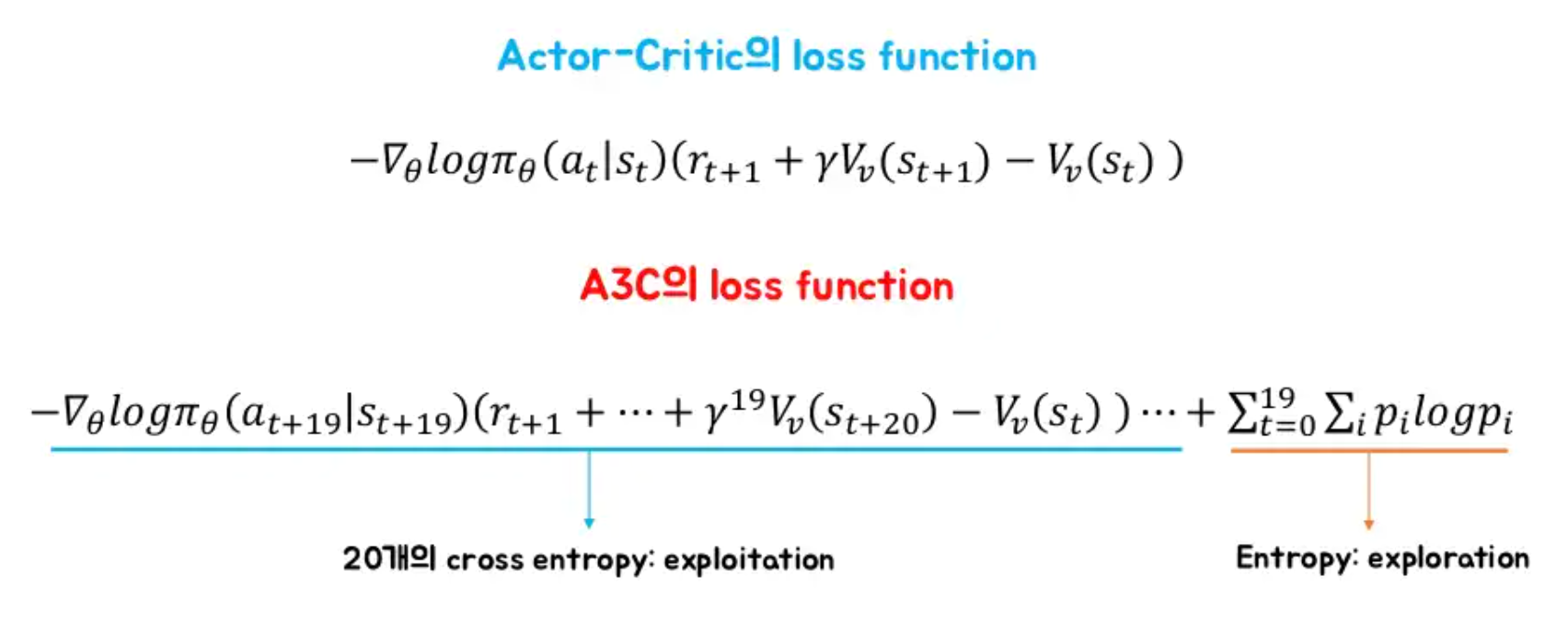
A3C
- Actor-Critic에서 나아가서, Actor를 업데이트하는 과정에서
- Multi-step loss function
- Entropy loss function
-
Multi-step : 20step 가본 후에 loss function이 하나 나오는 것 → 20step마다 20개의 loss function을 더한 것으로 업데이트
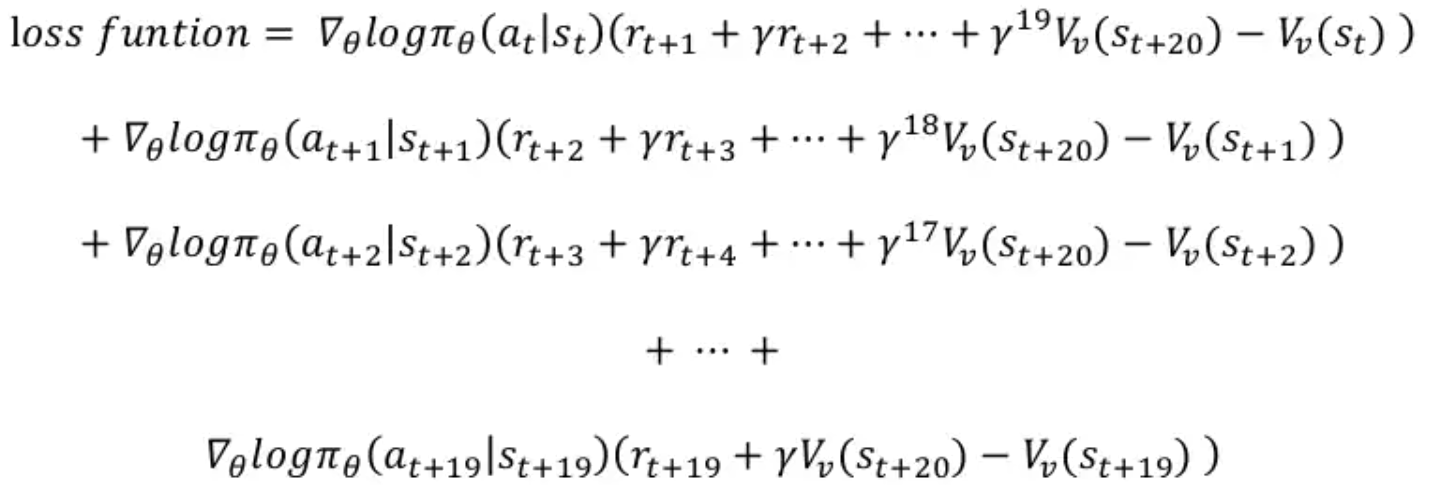
-
Entropy loss function
-
정리하면

Training Objective
- 이 부분은 보정된 EnergyPlus 시뮬레이터를 기반으로 난방 시스템에 대한 최적의 제어 정책을 훈련
- 최적의 제어 목표 : 허용 가능한 실내 열쾌적도 수준을 유지하면서 난방 수요를 최소화하는 것입니다.
- 열쾌적성 지표 : Fanger의 모델을 기반으로 한 PPD(Predicted Percentage of Dissatisfied)를 사용. PPD가 낮을수록 좋음
State Design
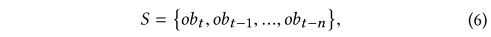
- t는 현재 제어 타임 스텝 , n은 고려할 과거 제어 타임 스텝 수, 각 ob는 15개 항목으로 구성됩니다. :
- 요일, 시간,
- 외기 온도(◦C), 외기 상대습도(%), 풍속(m/s), 풍향(북위도), 확산 일사량(W/m2), 직사 일사량(W/m2),
- 난방외기 온도 설정값(◦C), 평균 실내 공기 온도 설정값(◦C), 난방 시스템 급수 온도 설정값(◦C),
- 평균 실내 공기 온도(◦C), 평균 PPD(% - 열쾌적성지표), 점유 상태플래그,(0 or 1),
- 지난 타임 스텝 이후 평균 난방 수요( kW).
- 최소-최대 정규화는 각 항목을 0-1로 정규화하는 데 사용됩니다.
Action Design
A ={off, 20, 25, …, 65}
- Action은 DRL 에이전트가 환경을 제어하는 방법입니다.
- 이 연구에서 Action : 난방 시스템 급수 온도 설정값(◦C)
Reward Design
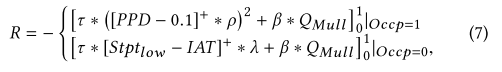
-
보상 설계는 제어 최적화 목표를 결정합니다.
-
난방 에너지 수요와 실내 열 쾌적성을 결합한 보상 함수는 식 (7)과 같습니다.
-
QMull은 지난 타임 스텝 이후 시스템 난방 수요(kW), Occp는 점유 상태 플래그,
-
τ, β, ρ, λ, Stptlow는 조정 가능한 하이퍼파라미터입니다.
-
τ 및 β는 최적화에서 Mullion 시스템 난방 수요 및 실내 열 쾌적성에 대한 가중치입니다.
-
ρ는 큰 PPD 값에 페널티를 주기 위한 스케일 팩터입니다.
-
λ는 비어 있는 시간 동안의 실내 온도 위반에 대한 패널티 수준이고,
-
Stptlow는 실내 공기 온도 패널티 임계값입니다.
-
- 모든 매개변수는 0과 1 사이에서 정규화됩니다.
-
보상 함수의 디자인은 더 나은 훈련 수렴 속도와 실내 열 쾌적성과 난방 수요 간의 균형을 위해 경험적으로 결정됩니다.
-
직관적으로, [PPD−0.1]+ 및 [Stptlow −IAT]+는 0.1(0.1은 공조기 표준 ASHRAE 에서 권장하는 임계값)보다 작은 PPD 값이나 Stptlow보다 높은 실내 공기 온도에 불이익을 주지 않습니다.
- PPD 항의 제곱은 0.1보다 큰 PPD 값에 페널티를 주기 위한 것입니다.
Training Setup
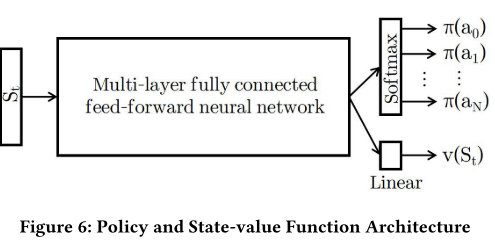
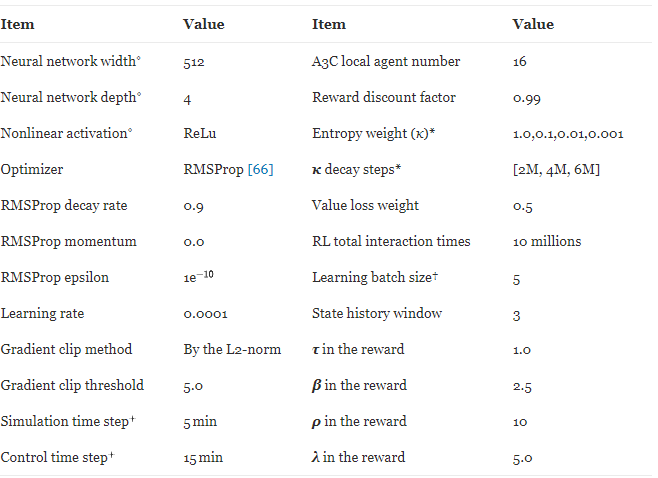
-
이 연구를 위한 신경망 아키텍처는 그림 6에 나와 있습니다. 공유 멀티레이어 피드포워드 신경망이 사용되며 공유 네트워크의 출력은 Softmax 레이어와 Linear 레이어에 병렬로 공급됩니다. 여기서 Softmax 계층은 제어 정책 분포(모든 행동에 대한 분포)를 출력하고 선형 계층은 상태 값을 출력합니다. 제어 행동은 제어 정책 배포에서 샘플링됩니다.
-
그림 6의 공유 네트워크에는 4개의 히든 레이어가 있으며 각 레이어에는 512개의 ReLu 유닛이 있습니다. RMSProp은 학습률 0.0001 및 RMSProp 감쇠 계수 0.9를 사용하여 최적화에 사용됩니다. 역전파의 그라디언트는 L2 norm ≤ 5.0으로 클리핑됩니다. 16 A3C 에이전트가 환경과 병렬로 상호 작용하기 위해 시작되고, 총 상호 작용 시간은 10M(에이전트당 ~ 600K)입니다. 상태 함수(State Design 식) 에서 히스토리 윈도우 n은 3입니다.
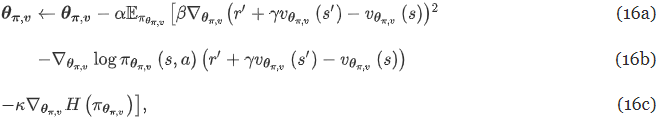
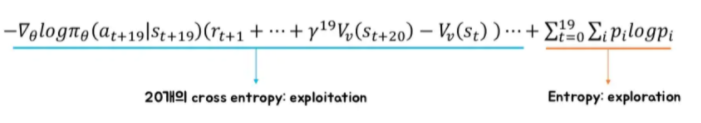
16a) Critic, 가치함수 v 근사
16b) Actor, 정책 근사
16c) 정책의 엔트로피 H(π_θ(s))는 에이전트의 무작위 탐색을 권장하는 데 사용됩니다. 하이퍼파라미터 κ는 탐색 수준을 제어하는 데 사용됩니다(값이 클수록 더 많은 탐색을 권장합니다). 이 연구에서 κ는 2M, 4M, 6M 및 10M 이전의 상호작용 단계에 대해 값이 1, 0.1, 0.05 및 0.01인 piece-wise 상수입니다.
What’s Next
Insight
- PG vs DQN ⇒ PG
- 빌딩 에너지 예측에서 action space는 연속적인 실수값이 많음.(온도 제어값, 밸브 제어 개도율 등) → “continous action spaces”
- DQN은 오직 이산적(discrete)이고 차원이 낮은 task에 유리→ action의 종류가 늘어날 수록 차원의 저주에 걸림
- 실제로 switch on/off 같은 제어값만 있는 주거용 스마트홈 에너지 예측은 DQN 아직 많이 쓰지만, 최근 빌딩 에너지 예측 연구들은 주로 DDPG 사용
- DDPG 적용 논문 리뷰 + DDPG 알고리즘 리뷰 필요
논문 리뷰 방향
- 위의 논문은 단기간(3개월)에 관찰된 데이터를 기반으로 보정되었기 때문에, 장기간에 취약.. 장기간 운영 데이터로 실증한 논문이 필요
- DDPG 적용 논문 리뷰 + DDPG 알고리즘 리뷰 필요
- 코드리뷰 병행
- Towards optimal control of air handling units using deep reinforcement learning and recurrent neural network(2020) - Building and Environment, reference count 21
- 2년 장기 운영데이터 사용
- LSTM + DDPG 사용
Reference
- A3C 설명 : RLCode와 A3C 쉽고 깊게 이해하기